Answer:
S12 for geometric series: 1.5+ (-3) + 6 +.... would be: -2047.5
Explanation:
Given the sequence to find the sum up-to 12 terms
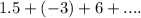
A geometric sequence has a constant ratio 'r' and is defined by
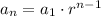
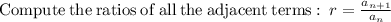
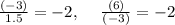
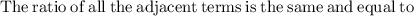
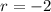
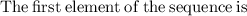
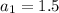
as
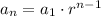
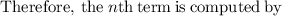
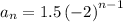
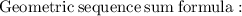
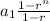
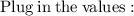
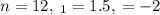
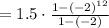
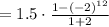
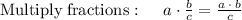
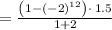
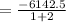 ∵
∵
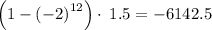
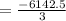
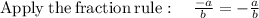
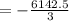
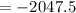
Thus, S12 for geometric series: 1.5+ (-3) + 6 +.... would be: -2047.5