the value of the discriminant of the quadratic equation
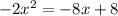 is
is
 .
.
Explanation:
Here we need to find What is the value of the discriminant of the quadratic equation -2x^2=-8x+8 or ,
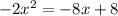 .
.
We know that for a quadratic equation ,
 , Discriminant is :
, Discriminant is :
⇒
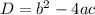
Now , let's frame equation
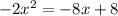 in form of
in form of
 :
:
⇒
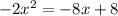
⇒

⇒
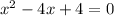
Comparing values we get that here , a=1 , b = -4 , c = 4 . Putting these values in
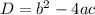 :
:
⇒
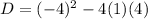
⇒
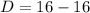
⇒

Therefore , the value of the discriminant of the quadratic equation
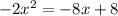 is
is
 .
.