Question

A clock is in the shape of a circle with radius r. The area A is given by the formula A=πr^2. Solve the formula for r. Then approximate the radius of the clock that has an area of 200 square inches.

Please help me and show me how to do it!!

Answer 1

7.97 inches.

Explanation:

Given the area of the clock is 200 sq inches.

#The clock is circular and its area is calculated using the formula:

`A=\pi r^2`

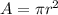
Where r is the clock's radius and
`\pi` is a constant(
`\pi=(22)/(7)=3.1429`)

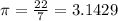#We substitute for
`\pi` and the given area(200 sq inches) in the area function to solve for r:

`A=\pi r^2\\\\200=\pi r^2\\\\r^2=(200)/(\pi)\\\\\#Take\ roots \ on \ both \ sides\\\\√(r^2)=\sqrt{(200)/(\pi)}\\\\r=\sqrt{(200)/(\pi)}\\\\=7.98 \ in`

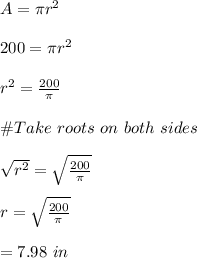
Hence, the clock's radius is 7.97 inches.