Question

The number of customers coming to a store during regualr work hours has an average of 15 customers/hour and follows a Poisson process. A customer walks in what is the probability that the next customer will not arrice for 5 minutes?

Answer 1

28.65% probability that the next customer will not arrive for 5 minutes

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

Mean of 15 customers an hour:

An hour has 60 minutes, so in the space of 5 minutes, the mean is:

`\mu = (15*5)/(60) = 1.25`

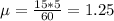
A customer walks in what is the probability that the next customer will not arrive for 5 minutes?

This is P(X = 0).

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(1.25)*(1.25)^(0))/((0)!) = 0.2865`

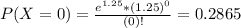
28.65% probability that the next customer will not arrive for 5 minutes