The given system of equations is
 and
and

We need to determine the solution to the system of equations.
Plotting the equation
 :
:
The equation
 can be plotted in the graph using the x and y intercepts.
can be plotted in the graph using the x and y intercepts.
When
 , the equation becomes
, the equation becomes

When
 , the equation becomes
, the equation becomes

Hence, joining these coordinates (0,-5) and (-1.25, 0), we get the line for the equation

Plotting the equation
 :
:
The equation
 can be plotted in the graph using the x and y intercepts.
can be plotted in the graph using the x and y intercepts.
When
 , the equation becomes
, the equation becomes
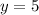
When
 , the equation becomes
, the equation becomes

Hence, joining these coordinates (0,5) and (-5,0), we get the line for the equation

Solution of the system of equations:
The solution of the system of equations is the point of intersection of these two lines.
Thus, from the graph, the lines intersect at the point (-2,3)
Hence, the solution to the system of equations is (-2,3)