Question

Applicants who wish to be admitted to a certain professional school in a large university are required to take a screening test devised by an educational testing service. From past results, the testing service has established that 70% of all applicants are eligible for admission and that 89% of those who are eligible for admission pass the exam, whereas 14% of those who are ineligible for admission pass the exam. (Round your answers to three decimal places.)

(a) What is the probability that an applicant for admission passed the exam?

(b) What is the probability that an applicant for admission who passed the exam was actually ineligible?

Answer 1

Probability of eligible applicants who pass the exam is 0.665

probability of applicants who are ineligible but pass the exam 0.063

Explanation:

Total percentage eligible applicants who pass the exam

`\textrm {89\% of 70\%}= (89*70)/(100)=62.3\%`

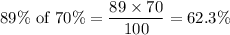
Total ineligible applicants who pass the exam

`\textrm {14\% of 30\%}= (14*30)/(100)=4.2\%`

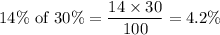
All applicants who pass this exam 62.3% + 4.2% = 66.5%

Probability of applicants who pass the exam

`\textrm{probability }= (66.5)/(100)=0.665`

Out of 66.5% applicants who pass the exam , 4.2% applicants are ineligible

`\textrm{so the probability is}(4.2)/(66.5)=0.063`

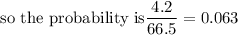
Probability of applicants who pass the exam is 0.665

probability of applicants who are ineligible but pass the exam 0.063