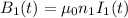Question

Consider first the generation of the magnetic field by the current I1(t)I1(t)I_{1}(t) in solenoid

1. Within the solenoid (sufficiently far from its ends), what is the magnitude B1(t) of the magnetic field due to this current?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

So the magnetic field on the solenoid 1 is would be

`B_1 (t) = \mu_0 n_1 I_1 (t)`

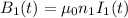
Step-by-step explanation:

Now in this question we are given an solenoid and our interest is on the magnetic field on the solenoid

Now first we will consider the Ampere's law which is mathematically represented as

∮
`\= B \cdot d \=s = \mu_0 I_(en)`

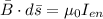
Where
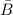`\=B` is the magnetic filed

∮ means the close integral

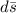`d\= s` is the length element

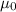`\mu_0` magnetic of permeability of free space

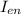`I_(en)` is the enclosed current

Now choosing a current path on a particular side of the solenoid (as shown on the second uploaded image) to evaluate the magnetic field

Where
`I` is the current elements within the enclosed current path

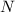`N` is the number of current elements in that particular enclosed current path.

and L is the length of enclosed path in the direction of the magnetic field as shown on the second uploaded image

So the integral of total path ∮
`\= B \cdot d \=s` =
`\int\limits { \= B } \, d\=s_1 + \int\limits { \= B } \, d\=s_2 +\int\limits { \= B } \, d\=s_3 +\int\limits { \= B } \, d\=s_4`

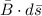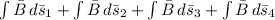
Where
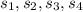`s_1 ,s_2 ,s_3,s_4` are the length element of each sides of the enclosed path

Now looking at the first integral we see that
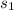`s_1` is moving the same direction with magnetic field B as shown on the third uploaded image

Now for
`s_2` the direction is perpendicular to the the direction of the magnetic field B so the value of magnetic field for that segment is 0 \

Now for
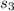`s_3` from the third uploaded image we see that there are no this segment so the value is zero

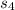`s_4` segment is the same as
`s_2` segment so the value of magnetic field on this segment is zero

Therefore

∮
`\= B \cdot d \=s` =
`BL + 0 + 0 + 0`

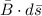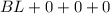
Now from Ampere's law ∮
`\= B \cdot d \=s = \mu_0 I_(en)`
`\equiv`
`BL = \mu_0 I_(en)`

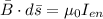
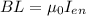
Now from the second uploaded image we see that
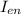`I_(en)` would now be equal to
`NI`

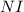
Therefore the equation becomes

`BL = \mu_0 (NI)`

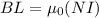
Now making B the subject we have

`B = (\mu_o NI)/(L) = \mu_0 (N)/(L) I`

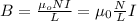
Now
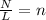`(N)/(L) = n` where n is the number of turns per length

So we have

`B = \mu_0 n I`

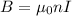
So the magnetic field on the solenoid 1 is would be

`B_1 (t) = \mu_0 n_1 I_1 (t)`