Question

I swear to god this is urgent:

A blimp provides aerial television views of a baseball game. The television camera sights the stadium at a 12° angle of depression. The altitude of the blimp is 300m. What is the​ line-of-sight distance from the television camera to the base of the stadium​? Round to the nearest hundred meters.

Answer 1

the​ line-of-sight distance from the television camera to the base of the stadium​ is 1449.28 m .

Explanation:

A blimp provides aerial television views of a baseball game. The television camera sights the stadium at a 12° angle of depression. The altitude of the blimp is 300 m. We need to find What is the​ line-of-sight distance from the television camera to the base of the stadium​ . Let's find out:

According to question , given scenario is in a right angle triangle where

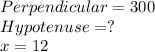`Perpendicular=300\\Hypotenuse=?\\x=12` , where x is angle of depression.

We know that
`sinx= (Perpendicular)/(Hypotenuse)`

⇒
`sin12= (300)/(Hypotenuse)`

⇒
`Hypotenuse= (300)/(Sin12)`

⇒
`Hypotenuse= (300)/(0.207)`

⇒
`Hypotenuse= 1449.28m`

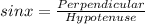
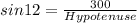
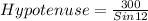
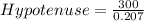
Therefore , the​ line-of-sight distance from the television camera to the base of the stadium​ is 1449.28 m .