Question

Geoffrey is evaluating the expression StartFraction (negative 3) cubed (2 Superscript 6 Baseline) Over (Negative 3) Superscript 5 Baseline (2 squared) EndFraction as shown below. StartFraction (negative 3) cubed (2 Superscript 6 Baseline) Over (Negative 3) Superscript 5 Baseline (2 squared) EndFraction = StartFraction (2) Superscript a Baseline Over (negative 3) Superscript b Baseline EndFraction = StartFraction c Over d EndFraction What are the values of a, b, c, and d? a = 4, b = 2, c = 16, d = 9 a = 4, b = negative 2, c = 16, d = 9 a = 8, b = 8, c = 256, d = 6,561 a = 8, b = 8, c = 256, d = negative 6,561

Answer 1

It is A.) a=4 b=2 c=16 d=9

Explanation:

I got a 100 on the test

Answer 2

The mathematical expression does not seem clear but I have made an attempt to make sense of what is implied.

Answer:

a = 4, b = 2, c = 16, d = 9

Explanation:

`((-3)^3(2^6))/((-3)^5(2^2)) = ((2)^a)/((-3)^b) = (c)/(d)`

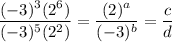
Solving the first part of the question by indices,

`((-3)^3(2^6))/((-3)^5(2^2)) = (-3)^(3-5)(2)^(6-2) = (-3)^(-2)(2)^(4) = ((2)^4)/((-3)^2)`

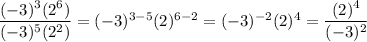
Comparing the rightmost term with the second term in the question,

a = 4, b = 2

Solving on,

`((2)^4)/((-3)^2) = ((2)*(2)*(2)*(2))/((-3)*(-3)) = (16)/(9)`

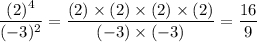
Comparing with the final term in the question,

c = 16 and d = 9

Therefore,

a = 4, b = 2, c = 16, d = 9