Answer:
The coordinates of the point on the line segment between A (3 , -5) and B (13 , -15) given that the point is 4/5 of the way from A to B would be: (11 , -13)
Explanation:
As the line segment has the points:
Let (x, y) be the point located on the line segment which is 4/5 of the way from A to B.
Using the formula
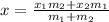
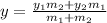
Here, the point (x , y) divides the line segment having end points (x₁, y₁) and (x₂, y₂) in the ratio m₁ : m₂ from the point (x₁, y₁).
As (x, y) be the point located on the line segment which is 4/5 of the way from A to B, meaning the distance from
 to
to
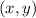 is
is
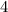 units, and the
units, and the
distance from
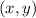 to B is 1 unit, as
to B is 1 unit, as
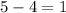 .
.
Thus
m : n = 4 : 1
so
Finding x-coordinate:
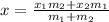
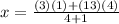
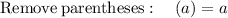
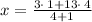
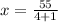 ∵
∵
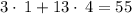
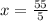
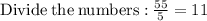
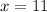
Finding y-coordinate:
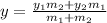
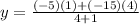
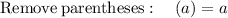

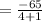 ∵
∵
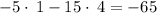
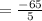
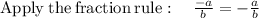
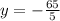
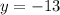
so
Therefore, the coordinates of the point on the line segment between A (3 , -5) and B (13 , -15) given that the point is 4/5 of the way from A to B would be: (11 , -13)