Answer:
the choice of a glider to hanging mass is a ratio of 20.2
Step-by-step explanation:
The Newton´s second law for glider is:
Fnet=Ma
T=Ma
The Newton´s second law for hanging mass is:
Fnet=ma
mag-T=ma
Replacing:
mag-Ma=ma (eq. 1)
Clearing a:
a=(mg)/(m+M)
The expression for motion is:

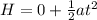
Clearing a:
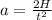
Replacing values:
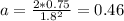
From eq. 1:
M/m=20.2