Answer: The pH at equivalence point for the given solution is 5.59.
Step-by-step explanation:
At the equivalence point,
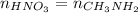
So, first we will calculate the moles of
 as follows.
as follows.
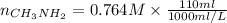
= 0.0845 mol
Now, volume of
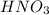 present will be calculated as follows.
present will be calculated as follows.
Volume =
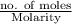
=
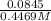
= 0.1891 L
Therefore, the total volume will be the sum of the given volumes as follows.
110 ml + 189.1 ml
= 299.13 ml
or, = 0.2991 L
Now,
![[CH_(3)NH_(3)^(+)] = (0.0845 mol)/(0.2991 L)](https://img.qammunity.org/2021/formulas/chemistry/college/bfyfntc2zrxfvdo2dys48wcn3y6rmp1er4.png)
= 0.283 M
Chemical equation for this reaction is as follows.
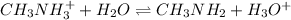
As,
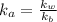
=
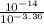
=
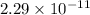
Now,
![[HNO_(3)] = \sqrt{k_(a)[CH_(3)NH_(3)^(+)]}](https://img.qammunity.org/2021/formulas/chemistry/college/fblkxhmrvnvfu2wb7epl3o4z38r5u1wi21.png)
=
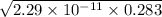
=
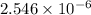
Now, pH will be calculated as follows.
pH =
![-log [H_(3)O^(+)]](https://img.qammunity.org/2021/formulas/chemistry/college/9fdo4m161hvcahrzz38e8lfcsk1h2xt1hn.png)
=
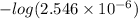
= 5.59
Thus, we can conclude that pH at equivalence point for the given solution is 5.59.