Question

The slope of AB is 3 over 4 and point A is (2. 9). How many possible locations are there for point

B? Which of the following describes a method to location the point?

Answer 1

Part 1) There are infinity locations for the point B

Part 2) see the explanation

Explanation:

Part 1) How many possible locations are there for point B?

we know that

The equation of a line in point slope form is equal to

`y-y1=m(x-x1)`

where

`m=(3)/(4)`

`(x1,y1)=(2,9)`

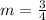
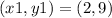
substitute

`y-9=(3)/(4)(x-2)`

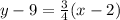
Convert to slope intercept form

`y-9=(3)/(4)x-(6)/(4)`

`y=(3)/(4)x-(6)/(4)+9`

`y=(3)/(4)x+(30)/(4)`

`y=0.75x+7.5`

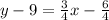
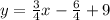
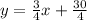
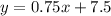
Point B can be any point ( different from point A) that satisfies the linear equation

therefore

There are infinity locations for the point B

Part 2) Describes a method to location the point

To locate the point, one of the two coordinates must be known. The known coordinate is placed into the linear equation and the equation is solved to find the value of the missing coordinate

Example

Suppose that the x-coordinate of point B is 4

For x=4

substitute in the linear equation

`y=0.75(4)+7.5=10.5`

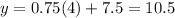
so

The coordinates of point B is (4,10.5)