the price per pound of the second type of the candy is 2.9 .
Explanation:
Here we have , After mixing two types of candies, the price became $3.40 per lb. The quantity of the first type of candy was 5/12 of the quantity of the second type. If the price of the first type of candy is $4.60 per lb,We need to find what is the price per pound of the second type of the candy . Let's find out:
The quantity of the first type of candy was 5/12 of the quantity of the second type i.e. Quantity of candy A = 5x quantity of candy B = 12x
We need to calculate the weighted average of the price of candies.
price of mixture = quantity of A (price of A ) + quantity of B (price of B)
⇒
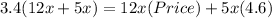
⇒
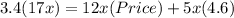
⇒
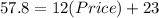
⇒
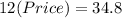
⇒
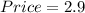
Therefor , the price per pound of the second type of the candy is 2.9 .