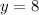2 Answers

Nate Sauber · Answer 1 · 2021-01-26T09:06:01+0000

Answer:

y = 8

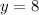
Explanation:

The given rational function is

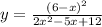
$y = \frac{ {(6 - x)}^(2) }{ {2x}^(2) - 5x + 12 }$

Let us expand the numerator to get;

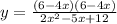
$y = \frac{(6 - 4x)(6 - 4x)}{2 {x}^(2) - 5x + 12 }$

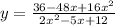
$y = \frac{36 - 48x + 16 {x}^(2) }{2 {x}^(2) - 5x + 12 }$

We can observe that, the degree of the numerator is the same as the degree of the denominator.

Therefore the horizontal asymptote is the ratio of the coefficient of the leading terms:

y = (16)/(2)

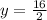
The horizontal asymptote is

y = 8

Please log in or register to add a comment.