Correct expression is
 . As n is greater then or equal to so circle will be closed . Correct options are B)
. As n is greater then or equal to so circle will be closed . Correct options are B)
 and D)The circle is closed.
and D)The circle is closed.
Explanation:
Here we have , Solve Negative two-thirds n less-than-or-equal-to 16. We need to find Which of the following must be true about the inequality and the resulting graph . Let's find out:
We have expression as :
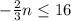
⇒
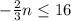
⇒
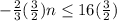
⇒
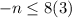
⇒

⇒
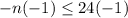
⇒

Therefore , Correct expression is
 . As n is greater then or equal to so circle will be closed . Correct options are B)
. As n is greater then or equal to so circle will be closed . Correct options are B)
 and D)The circle is closed.
and D)The circle is closed.