Question

Repost bc I forgot something.

You throw a football and it leaves your hand of 5 feet. Its initial velocity is 20 feet per second. What is the maximum height the ball will reach? Also, how long will it take the ball to hit the ground? (Equation used: h(t)= -16t^2 + v0t + h0.)
Please show work

Answer 1

The max height is 11.25 feet and the ball will take 1.464 seconds to hit the ground

Explanation:

The quickest way to solve this equation is by using the equation that you gave, which is h(t)= -16t^2 + v0t + h0. This equation models the trajectory of the football, which means that at the equation's vertex, we can model what the height of the ball is. Along with that, by finding the positive root of where h(t) = 0, we can find how long it will take for the ball to hit the ground.

First, lets find h0 and v(0)

h0 is the initial height of the ball. So we know that the ball leaves your hand of 5 feet, so h0 = 5. Similarly, the initial velocity is 20 ft/sec, so v0 = 20.

Plugging 5 in for h0 and 20 for v0, we get h(t) = -16t^2 + 20t + 5.

Second, find max height.

To find the vertex of a parabola, use -b/2a to find the time, and plug that into h(t) to get the height.

b=20

a=-16

t = -b/2a = -20/2(-16) = .625 seconds

h(.625) = 11.25 feet

The max height is 11.25 feet

Third, find how long.

To find this, we need to find the t-intercepts of the equation.

set h(t) = 0

-16t^2 + 20t + 5 = 0

Use quadratic formula to find t

t = (- 20 ±
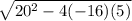`\sqrt{20^(2) - 4(-16)(5)}`)/2(-16)

t = {1.464}, -.214

The ball will take 1.464 seconds to hit the ground.