Question

A random sample of 45 professional football players indicated the mean height to be 6.18 feet with a sample standard deviation of 0.37 feet. A random sample of 40 professional basketball players indicated the mean height to be 6.45 feet with a standard deviation of 0.31 feet. Find a 95% confidence interval for the difference in mean heights of professional football and basketball players.

Answer 1

Explanation:

Hello!

The variables of interest are

X₁: height of a professional football player

n₁= 45

X[bar]₁= 6.18 feet

S₁= 0.37 feet

X₂: height of a professional basketball player

n₂= 40

X[bat]₂= 6.45 feet

S₂= 0.31 feet

You need to construct a 95%CI to estimate the difference between the mean heights of professional football players and basketball players.

To study the difference between the population means of two variables, you need these to have at least an approximately normal distribution. There is no information about the distributions of the variables so I'll assume that both study variables have a normal distribution and both population variances are equal.

The statistic you have to use to construct the interval is a t-test for independent samples with pooled sample variance:

(X[bar]₁-X[bar]₂)±
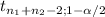`t_(n_1+n_2-2;1-\alpha /2)`*(Sa*
`\sqrt{(1)/(n_1) +(1)/(n_2) }`)

`t_(n_1+n_2-2;1-\alpha /2)= t_(45+40-2;1-0.025)= t_(83;0.975)= 1.989`

`Sa= \sqrt{((n_1-1)S^2_1+(n_2-1)S^2_2)/(n_1+n_2-2) }= \sqrt{(44*0.37^2+39*0.31^2)/(45+40-2) }=0.34`

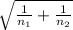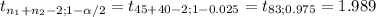
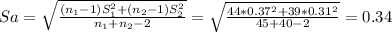
(6.18-6.45)±1.989*(0.34*
`\sqrt{(1)/(45) +(1)/(40) }`)

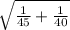[-0.42;-0.12]

With a 95% confidence level, you'd expect that the interval [-0.42;-0.12]feet with contain the difference between the average height of professional football and basketball players.

I hope you have a SUPER day!