Question

Find the extreme values of the function f(x, y) = 1x2 + 2y2 on the circle x2 + y2 = 1. SOLUTION We are asked for extreme values of f subject to the constraint g(x, y) = x2 + y2 = 1. Using Lagrange multipliers, we solve the equations ∇f = λ∇g and g(x, y) = 1, which can be written as fx = λgx fy = λgy g(x, y) = 1

Answer 1

Explanation:

Consider the function
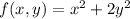`f(x,y) = x^2+2y^2`. Note that since the question does not ask to use the lagrange multipliers especificaly, another approach will be used.

NOte that we want to see the behavior of f over the restriction
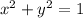`x^2+y^2=1`. That is either
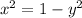`x^2=1-y^2` or
`y^2=1-x^2`.

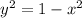Let us first replace the equality for x in the function f, then we get the following function

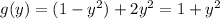`g(y) = (1-y^2)+2y^2 = 1+y^2`. This is a one variable function, so we can derive find the value of y for which the derivative is 0.

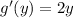`g'(y) = 2y`, if we equal it to zero, we get the value of y=0. If we use the second derivative criteria, we have that
`g''(y) = 2>0`, which tells us that y=0 is a minimum. Note that if y=0, then we have to critical points, which are (1,0) and (-1,0), both of them are point we f attains it's minimum.

On the other side, let us replace y in the function f on the same fashion. We get the function

`h(x) = x^2+2(1-x^2) = 2-x^2`.

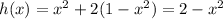REcall that

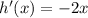`h'(x) = -2x` (hence x=0 gives us the critical point)

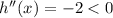`h''(x) = -2<0` (hence the critical point is a maximum).

This means that x=0 will give us the maximum for the function f. This occurs over the points (0,1) and (0,-1).