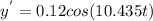Complete Question:
A mass of 150 g stretches a spring 9 cm. The mass is set in motion from its equilibrium position with a downward velocity of 12 cm/s and no damping is applied. Determine the position of the mass at any time . Use as the acceleration due to gravity. Pay close attention to the units.
Answer:
The position of the mass at any time = speed,
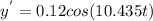
Step-by-step explanation:
Mass, m = 150 g = 150/1000 = 0.15 kg
Extension, x = 9 cm = 0.09 m
According to Hooke's law, F = kx...........(1)
F = mg........(2)
Equating (1) and (2)
mg = kx
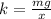
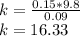
The differential equation that models the motion of a spring and a damper
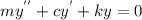
Since there is no damping applied, c = 0
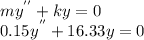
Solving the differential equation above by making
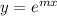 ,
,
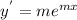 ,
,
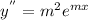
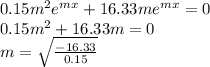
m = ± 10.435 i
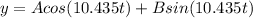
At the equilibrium position, t = 0, hence y = 0
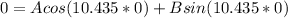 ..................(3)
..................(3)
A = 0
Inserting the value of A into equation (3)
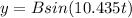 ...........(4)
...........(4)
The position of the mass at any time is equivalent to the speed of the spring
which is the first derivative of y
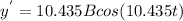 ..........(5)
..........(5)
Initial speed is given as 12 cm/s = 0.12 m/s, substituting this into equation (5)

Putting the value of B in equation (5)