Question

A survey of several 1010 to 1111 year olds recorded the following amounts spent on a trip to the mall: $18.31,$25.09,$26.96,$26.54,$21.84,$21.46$ 18.31,$ 25.09,$ 26.96,$ 26.54,$ 21.84,$ 21.46 Construct the 98%98% confidence interval for the average amount spent by 1010 to 1111 year olds on a trip to the mall. Assume the population is approximately normal.

Answer 1

Explanation:

Hello!

The variable of interest is

X: the amount a 10-11-year-old spends on a trip to the mall.

Assuming that the variable has a normal distribution, you have to construct a 98% CI for the average of the amount spent by the 10-11 year-olds on one trip to the mall.

For this you have to use a Student-t for one sample:

X[bar] ±
`t_(n-1;1-\alpha /2)` *
`(S)/(√(n) )`

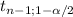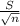
n= 6

`t_(n-1;1-\alpha /2)= t_(5; 0.99)= 3.365`

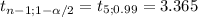
$18.31, $25.09, $26.96, $26.54, $21.84, $21.46

∑X= 140.20

∑X²= 3333.49

X[bar]= ∑X/n= 140.20/6= 23.37

S²= 1/(n-1)*[∑X²-(∑X)²/n]= 1/5[3333.49-(140.2)²/6]= 11.50

S= 3.39

X[bar] ±
`t_(n-1;1-\alpha /2)` *
`(S)/(√(n) )`

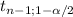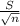
[23.37 ± 3.365 *
`(3.39)/(√(6) )`]

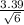[18.66;29.98]

With a confidence level of 98%, you'd expect that the interval $[18.66;29.98] will include the population mean of the money spent by 10-11 year-olds in one trip to the mall.

I hope you have a SUPER day!