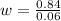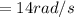Answer:
The angular velocity is
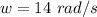 and the final velocity is v = 0.84 m/s
and the final velocity is v = 0.84 m/s
Step-by-step explanation:
From the question we are told that
The mass is
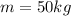
The diameter is
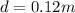
The radius is

The force is

The distance is
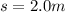
The force is mathematically represented as
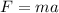
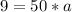
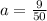
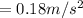
From the Equation of motion we have
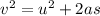
 is the final speed of the cable
is the final speed of the cable
substituting values we have
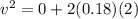
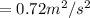
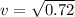
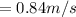
Now the linear velocity can be mathematically represented as
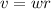
now substituting values
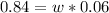
=>