Question

The following data represent the number of pods on a sample of soybean plants for two different plot types. Liberty Plot 32 31 36 35 44 31 39 37 38 No Till Plot 35 31 32 30 43 33 37 42 40 a. Find the mean yield for each plot type. b. Find the range of the yields for each plot type. c. Do parts a. and b. show any differences in the yields for the two plots

Answer 1

Explanation:

Hello!

You have the data corresponding to X: the number of pods on a sample of soybean planted in two different plot types ("Liberty" and "No-till")

Liberty Plot 32 31 36 35 44 31 39 37 38

No-Till Plot 35 31 32 30 43 33 37 42 40

a)

The mean of a sample is calculated by dividing the summation of all observations of the sample by its size: X[bar]= ∑X/n

Sample 1 Liberty plot:

X[bar]₁= ∑X₁/n₁=
`(32 + 31 + 36 + 35 + 44 + 31 + 39 + 37 + 38)/(9)= (248)/(9)= 27.56`

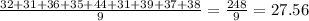
Sample 2 No Till plot:

X[bar]₂= ∑X₂/n₂=
`(35 + 31 + 32 + 30 + 43 + 33 + 37 + 42 + 40)/(9)= (323)/(9)= 35.89`

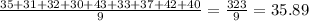
b)

The range of a variable is the interval between the max value and the min value of the variable, it shows you what is the possible dispersion of the values of the variable.

Sample 1:

Max₁: 44

Min₁: 31

R₁: Max₁ - Min₁ = 44 - 31 = 13

Sample 2

Max₂: 30

Min₂: 43

R₂= Max₂ - Min₂= 43 - 30= 13

c)

Sample 1 is centered in X[bar]₁= 27.56 and has a range of dispersion of R₁= 13

Sample 2 is centered in X[bar]₂= 35.59 and it has a range of dispersion of R₂= 13

Considering that the mean of sample 1 is less than the mean of sample 2 you could say that the average yield is greater in the "No-Till" plots.

Both data sets have the same range, this means that the variance of both plots is equal.

It seems that the yield for plots 2 "No-till" is better than the yield for plots 1 "Liberty"

I hope you have a SUPER day!