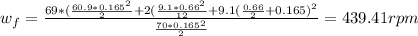Question

On average, both arms and hands together account for 13 % of a person's mass, while the head is 7.0 % and the trunk and legs account for 80 % . We can model a spinning skater with her arms outstretched as a vertical cylinder (head, trunk, and legs) with two solid uniform rods (arms and hands) extended horizontally. Suppose a 70.0 kg skater is 1.50 m tall, has arms that are each 66.0 cm long (including the hands), and a trunk that can be modeled as being 33.0 cm in diameter. If the skater is initially spinning at 69.0 rpm with her arms outstretched, what will her angular velocity ω 2 be (in rpm ) after she pulls in her arms and they are at her sides parallel to her trunk? Assume that friction between the skater and the ice is negligble.

Answer 1

Her angular velocity is 439.41 rpm

Step-by-step explanation:

The moment of inertia when her arms are at her side is

`I_(f) =(mr^(2) )/(2)`

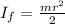
Where m=70 kg, r=33/2=0.165 m

The moment of inertia when her arms are stretched out is

`I_(i) =(m_(b)r^(2) )/(2) +2((m_(h)L^(2) )/(12)+m_(h) ((L)/(2)+r)^(2) )`

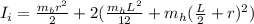
Where L=66 cm=0.66 m

mb= mass of body except hands=0.87*70=60.9 kg

mh= mass of hands+arms=0.13*70=9.1 kg

The conservation of angular momentum is:

Li=Lf

Ii*wi=If*wf

Clearing wf:

`w_(f) =(I_(i)w_(i) )/(I_(f) ) =(w_(i)((m_(b)r^(2) )/(2)+2((m_(h)L^(2) )/(12)+m_(h)((L)/(2)+r)^(2))) )/((mr^(2) )/(2) )`

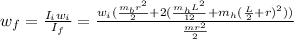
Replacing values:

`w_(f) =(69*((60.9*0.165^(2) )/(2)+2((9.1*0.66^(2) )/(12)+9.1((0.66)/(2)+0.165)^(2) )/((70*0.165^(2) )/(2) ) =439.41rpm`