Answer:
No, this result is not surprising. It is a little bit more than one standard deviation above 20%
Explanation:
Proportion of each color in the population (p) = 0.20
Sample size (n) = 20 Skittles
The standard deviation of a sampling distribution is determined by:
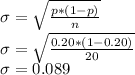
The difference between the observed proportion of 0.30, and the mean proportion of 0.20 is 0.10, which is just a little bit more than one standard deviation of 0.089. Therefore, this result is not surprising since it is a little bit more than one standard deviation above 20%.