Answer:
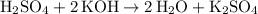 .
.
Step-by-step explanation:
Indeed it is possible to solve this problem with system of multiple equations. This explanation will give an approach that gives the same result with less calculations.
Start by finding the most complex species in the equation and setting its coefficient to
 . That species should as many elements as possible. For example, in this question,
. That species should as many elements as possible. For example, in this question,
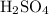 ,
,
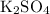 , and
, and
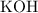 all contain three elements each. Nonetheless,
all contain three elements each. Nonetheless,
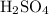 and
and
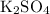 are more preferable for they contain more atoms.
are more preferable for they contain more atoms.
For example, in case
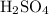 is chosen as the most complex species. Set its coefficient to
is chosen as the most complex species. Set its coefficient to
 :
:
 .
.
There are two
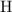 atoms, one
atoms, one
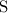 atom, and four
atom, and four
 atoms in that
atoms in that
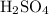 . Since
. Since
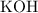 also contains
also contains
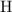 and
and
 , it is not certain how many
, it is not certain how many
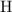 and
and
 on the left-hand side in total. However, on the left-hand side,
on the left-hand side in total. However, on the left-hand side,
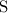 appears only in
appears only in
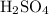 . Therefore, it is certain that there is only one
. Therefore, it is certain that there is only one
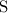 in the left-hand side of the equation.
in the left-hand side of the equation.
In chemical reaction, atoms of an element are neither created nor destroyed. Therefore, the number of
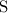 atoms on the right-hand side should be the same as that on the left-hand side. Therefore, there should also be only one
atoms on the right-hand side should be the same as that on the left-hand side. Therefore, there should also be only one
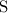 atom on the right-hand side.
atom on the right-hand side.
On the right-hand side,
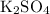 is the only compound that contains
is the only compound that contains
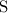 . Besides, each formula unit of
. Besides, each formula unit of
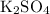 contains exactly one
contains exactly one
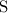 . The only way to get exactly one
. The only way to get exactly one
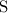 atom on the right-hand side is to set the coefficient of
atom on the right-hand side is to set the coefficient of
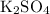 to one, as well. The equation will then look like:
to one, as well. The equation will then look like:
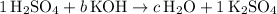 .
.
With a similar logic, on the right-hand side,
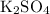 is the only species with
is the only species with
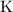
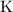 atoms. There would be exactly two
atoms. There would be exactly two
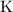 atoms on each side of the equation. On the left-hand side,
atoms on each side of the equation. On the left-hand side,
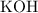 is the only species with
is the only species with
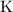 atoms. Each formula unit of
atoms. Each formula unit of
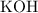 contains one
contains one
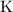 atom. Therefore, the coefficient of
atom. Therefore, the coefficient of
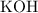 should be
should be
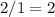 .
.
 .
.
It is now certain that there are
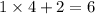 (six)
(six)
 atoms on the left-hand side of the equation. With a similar logic, there should also be six
atoms on the left-hand side of the equation. With a similar logic, there should also be six
 atoms on the right-hand side of the equation. Four of these would come from
atoms on the right-hand side of the equation. Four of these would come from
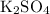 . The other two would come from
. The other two would come from
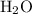 .
.
Each
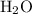 molecule contains one
molecule contains one
 atom. As a result, there needs to be
atom. As a result, there needs to be
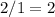 (two)
(two)
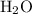 molecules on the left-hand side.
molecules on the left-hand side.
Hence the equation:
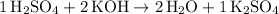 .
.
Double-check the work by making sure that the number of
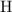 atoms is also the same on both sides of the equation.
atoms is also the same on both sides of the equation.