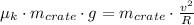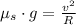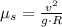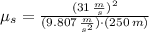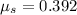Question

A crate is being transported in the horizontal bed of a pick-up truck. (a) When the truck reaches a speed of 31.0 m/s as it is taking a turn on a horizontally flat part of the highway which has a radius 250 m, the crate starts sliding sideways. Calculate the coefficient of static friction between the crate and the truck bed.

Answer 1

`\mu_(s) = 0.392`

Step-by-step explanation:

Let assume that road has no inclination. The pick-up truck experiments a centripetal force as net force, whereas the crate has a centrifugal one by the Newton's 3rd Law. The crate starts moving when
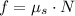`f = \mu_(s)\cdot N`. The crate is modelled by the following equations of equilibrium:

`\Sigma F_(r) = \mu_(s)\cdot N = m_(crate)\cdot (v^(2))/(R)`

`\Sigma F_(n) = N - m_(crate)\cdot g = 0`

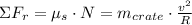
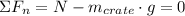
After some handling, the coefficient of static friction is determined:

`\mu_(k) \cdot m_(crate) \cdot g = m_(crate)\cdot (v^(2))/(R)`

`\mu_(s)\cdot g = (v^(2))/(R)`

`\mu_(s) = (v^(2))/(g\cdot R)`

`\mu_(s) = ((31\,(m)/(s) )^(2))/((9.807\,(m)/(s^(2)) )\cdot (250\,m))`

`\mu_(s) = 0.392`