Question

Water flows through a tee in a horizontal pipe system. The velocity in the stem of the tee is 15 f t/s, and the diameter is 12 in. Each branch is of 6 in diameter. If the pressure in the stem is 20 psi, calculate magnitude and direction of the force of the water on the tee if the flow rate in the branches are the same

Answer 1

The resultant force is 2620.05 lbf acting to the right.

Step-by-step explanation:

The area for inlet section is:

`A_(1)=(\pi D_(1)^(2) )/(4) =(\pi (12/12)^(2) )/(4) =0.79 ft^(2)`

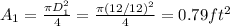
The area for oulet section is:

`A_(2) =(\pi D_(2)^(2) )/(4) =(\pi (6/12)^(2) )/(4) =0.196 ft^(2)`

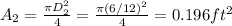
The volumetric flow rate is:

Q=V1A1=15*0.79=11.85 ft^3/s

The velocities and areas at the exit is the same:

Q=V2A2+V3A3=2V2A2

Clearing V2:

V2=V3=Q/(2*A2)=11.85/(2*0.196)=30 ft/s

The mass flow rate through inlet is:

m1=ρA1V1=1.94*15*0.79=22.99 lbf*s/ft

The mass flow rate through outlet is:

m2=m3=m1/2=22.99/2=11.49 lbf*s/ft

The x-component of force is:

Rx+p1A1=-V1m1

Where p1 is the pressure at inlet

Rx=-(15*22.99)-(2880*0.79)=-2620.05 lbf

Fx=-Rx=2620.05 lbf

The y-component of force is:

Ry+p2A2-p3A3=V2m2-V3m3

Ry+0-0=(30*11.49)-(30*11.49)

Ry=0

Fy=Ry=0

The resultant force is:

`F=\sqrt{Fx^(2)+Fy^(2) } =\sqrt{2620.05^(2)+0 } =2620.05 lbf`

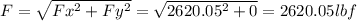
This force is acting to the right.