Answer:
v = 0.999981c m/s
Step-by-step explanation:
Using the time dilation equation
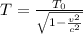
T = stationary time = 100 years
T₀ = 11/12 years = 0.917 years
v = speed of travel in the space = ?
c = speed of light = 3 * 10⁸ m/s
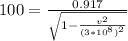
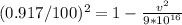
v = 299987395.57 m/s
v = 2.99 * 10⁸ m/s
v = 0.999981c m/s