Question

Suppose that the loan amount on mortgages for a particular zip code is normally distributed with a mean of 154,449, measured in dollars, with a standard deviation of 14,794. What is the z value for a loan of 162,443 dollars? Answer to three decimal places if needed.

Answer 1

The z value for a loan of 162,443 dollars is 0.5404.

Explanation:

We are given that the loan amount on mortgages for a particular zip code is normally distributed with a mean of 154,449, measured in dollars, with a standard deviation of 14,794.

Let X = loan amount on mortgages for a particular zip code

So, X ~ N(
`\mu=154,449,\sigma^(2)=14,794^(2)`)

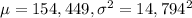Now, the z score probability distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean loan amount = $154,449

`\sigma` = standard deviation = $14,794

So, the z-score for a loan of 162,443 dollars is given by;

Z =
`(162,443 - 154,449)/(14,794)`

=
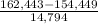
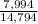`(7,994)/(14,794)` = 0.5404

Therefore, the z value for a loan of 162,443 dollars is 0.5404.