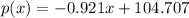Question

Use the given data to find a regression line that best fits the price-demand data for price p in dollars as a function of the demand x widgets. Here, price is the dependent variable, and demand is the independent variable. Find the regression function for price, and write it as p ( x )

Answer 1

`m=-(7600)/(8250)=-0.921`

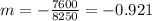
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(550)/(10)=55`

`\bar y= (\sum y_i)/(n)=(1042)/(10)=104.2`

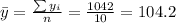
And we can find the intercept using this:

`b=\bar y -m \bar x=104.2-(-0.921*55)=104.707`

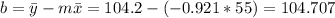
So the line would be given by:

`y=-0.921 x +104.707`

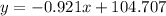
Explanation:

For this case we have the following data given:

Demand (x): 10,20,30,40,50,60,70,80,90,100

Price (y): 141 , 133,126, 128,113,97, 90, 82,79,53

We want to construct a linear model like this:

`y = mx +b`

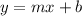
For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

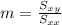
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

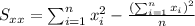
So we can find the sums like this:

`\sum_(i=1)^n x_i =550`

`\sum_(i=1)^n y_i =1042`

`\sum_(i=1)^n x^2_i =38500`

`\sum_(i=1)^n y^2_i =115882`

`\sum_(i=1)^n x_i y_i =49710`

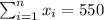
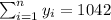
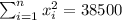
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=38500-(550^2)/(10)=8250`

`S_(xy)=\sum_(i=1)^n x_i y_i -\frac{(\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i)}=49710-(550*1042)/(10)=-7600`

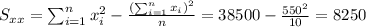
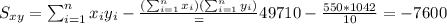
And the slope would be:

`m=-(7600)/(8250)=-0.921`

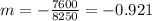
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(550)/(10)=55`

`\bar y= (\sum y_i)/(n)=(1042)/(10)=104.2`

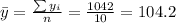
And we can find the intercept using this:

`b=\bar y -m \bar x=104.2-(-0.921*55)=104.707`

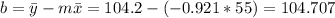
So the line would be given by:

`p(x)=-0.921 x +104.707`