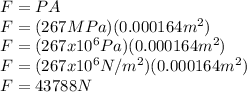Question

or a bronze alloy, the stress at which plastic deformation begins is 267 MPa and the modulus of elasticity is 115 GPa. (a) What is the maximum load (in N) that may be applied to a specimen having a cross-sectional area of 164 mm2 without plastic deformation

Answer 1

The maximum load (in N) that may be applied to a specimen with this cross sectional area is
`F=43788 N`

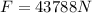
Step-by-step explanation:

We know that the stress at which plastic deformation begins is 267 MPa.

We are going to assume that the stress is homogeneously distributed. As a definition, we know that stress (P) is force (F) over area(A), as follows:

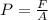`P=(F)/(A)` (equation 1)

We need to find the maximum load (or force) that may be applied before plastic deformation. And the problem says that the maximum stress before plastic deformation is 267 MPa. So, we need to find the value of load when P= 267 MPa.

Before apply the equation, we need to convert the units of area in
`m^(2)`. So,

`A[m^(2)]=A[mm^(2) ]((1 m)/(1000 mm)) ^(2)\\A[m^(2)]=164 mm^(2)((1 m)/(1000 mm))^(2) \\A[m^(2)]=0.000164 m^(2)`

And then, from the equation 1,

`F=PA\\F=(267 MPa)(0.000164 m^(2))\\F=(267x10^(6) Pa)(0.000164 m^(2))\\F=(267x10^(6) N/m^(2))(0.000164 m^(2))\\F=43788 N`