Answer:
a)
 , b)
, b)
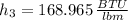 , c)
, c)

Step-by-step explanation:
a) The tank can be modelled by the Principle of Mass Conservation:

The mass flow rate exiting the tank is:
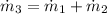
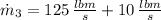

b) An expression for the specific enthalpy at outlet is derived from the First Law of Thermodynamics:
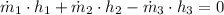
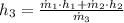
Properties of water are obtained from tables:
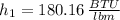
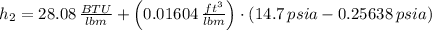

The specific enthalpy at outlet is:
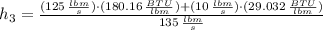
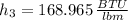
c) After a quick interpolation from data availables on water tables, the final temperature is:
