Answer:
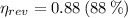 ,
,
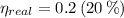
Step-by-step explanation:
The Carnot efficiency is the maximum theoretical efficiency that a thermal machine can reach, the expression is:
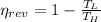
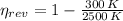
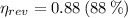
The real efficiency of the engine is:
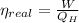
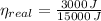
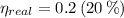
Real efficiency of the engine must be lower than maximum theoretical efficiency due to irreversibilities.