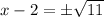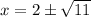Question

Solve x

2 - 4x - 7 = 0 by completing the square. What are the solutions?

{2 + , 2 - }
{-2 + , -2 - }
{2 + , 2 + }

Answer 1

Explanation:

`x^(2) - 4x - 7 = 0`

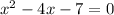
First, let's move the
`7` to the right-hand side so we can determine what constant we'll need on the left-hand side to complete the square:

`x^(2) - 4x = 7`

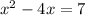
From here, since the coefficient of the
`x` term is
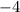`-4`, we know the square will be
`(x - 2)` (since
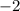`-2` it's half of
`-4`).

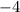To complete this square, we will need to add
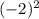`(-2)^(2)` to both sides of the equation:

`x^(2) - 4x + (-2)^2 = 7 + ^(-2)`

`x^(2) - 4x + 4 = 7 + 4`

`(x - 2)^(2) = 11`

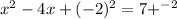
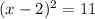
Now we can take the square root of both sides to figure out the solutions to
`x`:

`x - 2 = \pm √(11)`

`x = 2 \pm √(11)`