Question

A "swing" ride at a carnival consists of chairs that are swung in a circle by 19.6 m cables attached to a vertical rotating pole, as the drawing shows. Suppose the total mass of a chair and its occupant is 250 kg. (a) Determine the tension in the cable attached to the chair. (b) Find the speed of the chair.

Answer 1

Step-by-step explanation:

Given that,

Length of the cable is 19.6 m, l = 19.6 m

Let us assume that the angle with vertical rotating pole is 62.5 degrees.

The total mass of a chair and its occupant is 250 kg.

(a) Let T is the tension in the cable attached to the chair. So,

`T\cos\theta=mg\\\\T=(mg)/(\cos\theta)\\\\T=(250* 9.8)/(\cos(62.5))\\\\T=5305.91\ N`

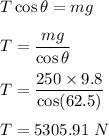
(b) The centripetal acceleration is balanced by :

`(v^2)/(r)=g\tan\theta\\\\v=√(Rg\tan\theta) \\\\v=√(l\sin\theta g\tan\theta)\\\\v=√(19.6* \sin(62.5)9.8* \tan(62.5))\\\\v=18.09\ m/s`

Hence, this is the required solution.

Answer 2

Step-by-step explanation:

radius, R = 19.6 m

mass, m = 250 kg

(a) The tension in the cable is T.

T = mg

T = 250 x 9.8

T = 2450 N

(b) Let v is the speed of the chair.

the tension force is balanced by the centripetal force.

T = mv²/r

2450 = 250 x v²/19.6

v² = 192.08

v = 13.86 m/s

Thus, the speed of the car is 13.86 m/s