Answer:
The 99% confidence interval is (0.508, 0.726).
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
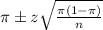
In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
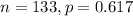
99% confidence level
So
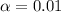 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
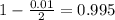 , so
, so
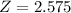 .
.
The lower limit of this interval is:
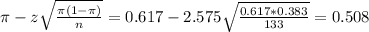
The upper limit of this interval is:
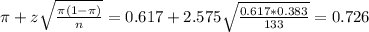
The 99% confidence interval is (0.508, 0.726).