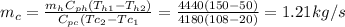Question

Hot engine oil with heat capacity rate of 4440 W/K (product of mass flow rate and specific heat) and an inlet temperature of 150ºC flows through a double pipe heat exchanger. The double pipe heat exchanger is constructed using a 1.5-m-long copper pipe (k = 250 W/m.K) with an inner tube of inside diameter 2 cm and outside tube diameter of 2.25 cm. The inner diameter of the outer tube of the double pipe heat exchanger is 6 cm. Oil flowing at a rate of 2 kg/s through inner tube exits the heat exchanger at a temperature of 50ºC. The cold fluid, i.e., water enters the heat exchanger at 20ºC and exits at 108ºC. Assume the fouling factor on the oil side and water side to be 0.00015 m2.K/W and 0.0001 m2.K/W, respectively.

The properties of water evaluated at an average temperature at the average inlet and exit temperatures of 20ºC and 70ºC or 45ºC are

rho = 990.1kg/m^3
Cp= 4180J/kg.K
k= 0.637W/m.K
μ= 0. 596 ×10^-3 kg/m.s
Pr = 3.91

Calculate the mass flow rate of water.(Round the answer to three decimal places.)

Answer 1

The mass flow rate of water is 1.21 kg/s

Step-by-step explanation:

according to the conditions given in the exercise:

mhcp=4440 W/K

Th1=150°C

Th2=50°C

Tc1=20°C

Tc2=108°C

di=2 cm

do=2.25 cm

Di=6 cm

mh=2 kg/s

Rfo=0.00015 m^2K/W

Rfi=0.0001 m^2K/W

The properties of the water at 45°C are:

p=990.1 kg/m^3

Cp=4180 J/kgK

From the energy balance, we have:

mc*Cpc(Tc2-Tc1)=mh*Cph(Th1-Th2)

Clearing mc:

`m_(c)=(m_(h)C_(ph)(T_(h1)-T_(h2)) )/(C_(pc)(Tc_(2)-Tc_(1) )=(4440(150-50))/(4180(108-20)) =1.21 kg/s`