Question

A college student with a bachelors degree in nursing from an accredited institution has an 86.74% chance of getting hired full time in a hospital setting within 6 months of graduation. There is a 34.72% chance of a student interested in a nursing degree not making it through the program due to not meeting GPA requirements, finding another health science track they'd rather complete, or various other reasons. Compute the probability of a Madonna University nursing student getting hired within 6 months of graduation given that they complete their degree here.

Answer 1

86.74% probability of a Madonna University nursing student getting hired within 6 months of graduation given that they complete their degree here.

Explanation:

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

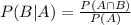
In which

P(B|A) is the probability of event B happening, given that A happened.

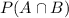`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

Compute the probability of a Madonna University nursing student getting hired within 6 months of graduation given that they complete their degree here.

In this problem, we have that:

Event A: Completing their degree there.

There is a 34.72% chance of a student interested in a nursing degree not making it through the program.

So 100 - 34.72% = 65.28% = 0.6528 probability of completing their degree. So P(A) = 0.6528.

Event B: Getting hired

86.74% chance of getting hired full time in a hospital setting within 6 months of graduation.

Completing their degree and getting hired:

`P(A \cap B) = 0.6528*0.8674`

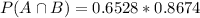
Probability:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.6528*0.8674)/(0.6528) = 0.8674`

86.74% probability of a Madonna University nursing student getting hired within 6 months of graduation given that they complete their degree here.