Question

A 10 kg block is pulled across a horizontal surface by a rope that is oriented at 60° relative to the horizontal surface. What is the work (in J) done by the tension in the rope if the block is dragged 10 m at constant velocity? The coefficient of kinetic friction between the block and the floor is 0.2 and you may assume that the magnitude of the tension is constant as the block is pulled.

Answer 1

145.6 J work is done by the tension.

Step-by-step explanation:

Given:

Mass of the block (m) = 10 kg

Displacement of the block (d) = 10 m

Coefficient of kinetic friction (μ) = 0.2

Angle between the tension force and the displacement (x) = 60°

The block is moving with a constant velocity.

We know that, if a body moves with a constant velocity, then the acceleration of the body is zero as acceleration is the rate of change of velocity.

Now, from Newton's second law, the net force acting on a body is directly proportional to its acceleration. So, if acceleration of the block is zero, then the net force acting on the block is also zero.

Here, the forces acting on the block along the direction of motion of block are:

1. Component of tension force in the direction of displacement.
2. Frictional force in the direction opposite to displacement.

Now, as the net force is zero, both the forces stated above must be equal in magnitude.

Therefore, the tension component in the direction of displacement is given as:

`T_x=T\cos x`

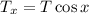
Where, 'T' is the tension in the rope.

`T_x=T* 0.5=0.5T----(1)`

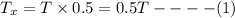
Now, consider the vertical direction. There is no motion in the vertical direction. So, net force is zero or net upward force is equal to net downward force. This gives,

`T_y+N=mg\\\\T\sin x+N=mg\\\\N=mg-T\sin x\\\\N=10* 9.8-T\sin 60^\circ\\\\N=98-(\sqrt3T)/(2)-------(2)`

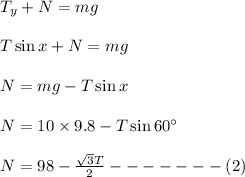
Now, frictional force is given as:

`f=\mu N\\\\f=0.2N`

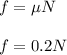
From equation (2), we get:

`f=0.2(98-(\sqrt3)/(2)T)\\\\f=19.6-(\sqrt3T)/(10)-------(3)`

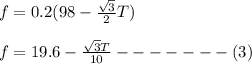
Now, as net force in horizontal direction is zero, we have:

`T_x=f`

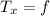
From equations (1) and (3), we have:

`0.5T=19.6-(\sqrt3T)/(10)\\\\0.5T+(\sqrt3T)/(10)=19.6\\\\0.673T=19.6\\\\T=29.12\ N`

Now, work done is given as:

Work = Force × Displacement × cos x

`W=Td\cos x\\\\W=29.12* 10* \cos 60^\circ\\\\W=145.6\ J`

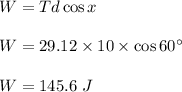
Therefore, 145.6 J work is done by the tension.