Question

Your film idea is about drones that take over the world. In the script, two drones are flying horizontally at the same speed and direction, one directly above the other. Suddenly, the drone on top malfunctions and loses power. It falls and collides with the drone below. Just before the collision, the falling drone has a vertical component of velocity of 60 m/s, while maintaining its horizontal component of velocity. The falling drone has a mass of 1 kg and the bottom drone has a mass of 3 kg. Before the malfunction, both drones were traveling horizontally with a speed of 20 m/s. If the two drones stick together after the collision, find the final speed and direction of the two drones just after the collision. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Answer 1

vₓ = 20 m/s, v_{y} = -15 m / s

Step-by-step explanation:

This is a conservation of moment problem, since it is a vector quantity we can work each axis independently

The system is formed by the two drones, so the forces during the crash are internal and the moment is conserved

X axis

Initial moment. Before the crash

p₀ = m₁ v₀ₓ + m₂ v₀ₓ

Final moment. After the crash

p_{fx} = (m₁ + m₂) vₓ

p₀ₓ =
`p_(fx)`

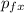
m₁ v₀ₓ + m₂ v₀ₓ = (m₁ + m₂) vₓ

vₓ = (m₁ + m₂) v₀ₓ / (m₁ + m₂)

vₓ = v₀ₓ = 20 m/s

Y Axis

Initial

p_{oy} = m₁ v_{oy}

Final

p_{fy} = (m₁ + m₂) v_{y}

p_{oy} = p_{fy}

the drom rises and when it falls it has the same speed because there is no friction v_{oy} = -60 m/s

m₁
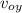`v_(oy)` = (m₁ + m₂) v_{y}

v_{y} = m₁ / (m₁ + m₂) v_{oy}

v_{y} = 1/4 60

v_{y} = -15 m / s

Vertical speed is down