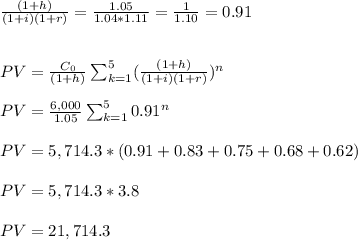Answer:
The equivalent present worth of the series is $27,714.
Step-by-step explanation:
We have a series of five payments (n=5), paid at the end of the year, starting with $6,000 and increasing at a rate of 5% per year.
The inflation rate is 4% and the market interest rate is 11%.
The equivalent present worth of the series, where we take into account yearly increments and discount the value by inflation and interest rate, is:

Where:
h: increment in the payments (5%)
i: rate of inflation (4%)
r: market interest rate (11%)
Then,