Question

Brian can get to class by taking either a Commuter North bus, a Bursley Baits bus, or a Northwood Express bus. If he takes Commuter North, there is a 50% chance he is late. If he takes Bursley Baits, there is a 20% chance he is late. If he takes Northwood Express, there is a 5% chance he is late. a) Assume there is an equal probability of taking any given bus. Given that Brian is late to class, what is the probability Brian took a Commuter North bus? b) Assume Brian takes Commuter North 30% of the time, takes Bursley Baits 10% of the time, and takes Northwood Express 60% of the time. Given that Brian was not late to class, what is the probability that he took a Commuter North bus?

Answer 1

a. The probability that Brian took a Commuter North bus (given that Brian is late to class) is
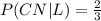`\\ P(CN|L) = (2)/(3)`; b. The probability that Brian took a Commuter North bus (given that he was not late) is
`\\ P(CN|\overline{L}) = 0.1875`.

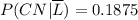Step-by-step explanation:

This is a case of the Bayes' Theorem and we have conditional probabilities here.

We need to start to define each event:

1. The event of taking a Commuter North bus, CN.
2. The event of taking a Bursley Baits bus, BB.
3. The event of taking a Northwood Express, NE.
4. The event of being late, L.

The question tells us important information to solve it:

"If he takes Commuter North, there is a 50% chance he is late". This is a conditional probability that can be written as P(L | CN) = 0.50. That is, given that Brian gets the Commuter North, the probability of being late is 0.50.

We can proceed similarly with the remaining conditional probabilities.

"If he takes Bursley Baits, there is a 20% chance he is late" or P(L | BB) = 0.20.

"If he takes Northwood Express, there is a 5% chance he is late" or P(L | NE) = 0.05.

Given that Brian is late to class, what is the probability Brian took a Commuter North bus?

We have to assume in this part that there is "an equal probability of taking any given bus". So,
`\\ P(CN) = P(BB) = P(NE) = (1)/(3)`.

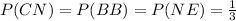Then, the probability of being late is as follows:

`\\ P(L) = P(L|CN)*P(CN) + P(L|BB)*P(BB) + P(L|NE)*P(NE)`

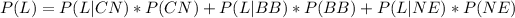
This is because we have three different events and we have to take into account the simultaneous probabilities of the events L an CN, L and BB, and L and NE. We have to remember that the conditional probability formula is as follows:

`\\ P(A|B) = (P( A \cap B))/(P(B))`

`\\ P(A|B)*P(B) = P( A \cap B)`

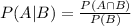
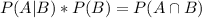
Then

`\\ P(L) = P(L|CN)*P(CN) + P(L|BB)*P(BB) + P(L|NE)*P(NE)`

`\\ P(L) = 0.50*(1)/(3) + 0.20*(1)/(3) + 0.05*(1)/(3)`

`\\ P(L) = (1)/(3)*(0.50 + 0.20+ 0.05)`

`\\ P(L) = (1)/(3)*(0.75)`

`\\ P(L) = (1)/(3)*(3)/(4)`

`\\ P(L) = (1)/(4) = 0.25`

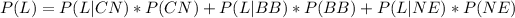
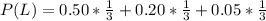
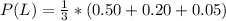
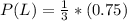
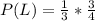
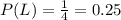
The question is asking for

`\\ P(CN|L) = (P(CN \cap L))/(P(L))`. But

`\\ P(CN \cap L) = P(L \cap CN) = P(L|CN)*P(CN)`

Then

`\\ P(CN|L) = (P(L|CN)*P(CN))/(P(L))`

`\\ P(CN|L) = ((1)/(2)*(1)/(3))/((1)/(4))`

`\\ P(CN|L) = ((1)/(6))/((1)/(4))`

`\\ P(CN|L) = (4)/(6)`

`\\ P(CN|L) = (2)/(3) \approx 0.6666...`

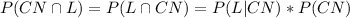
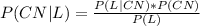
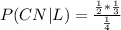
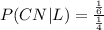
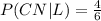
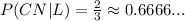
Then, the probability that Brian took a Commuter North bus (given that Brian is late to class) is
`\\ P(CN|L) = (2)/(3)`.

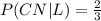Given that Brian was not late to class, what is the probability that he took a Commuter North bus?

We can proceed similarly as the previous answer. But the conditional probabilities of not being late are complementary to those of being late.

`\\ P(\overline{L}|CN) = 1 - 0.50 = 0.50`

`\\ P(\overline{L}|BB) = 1 - 0.20 = 0.80`

`\\ P(\overline{L}|NE) = 1 - 0.05 = 0.95`

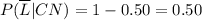
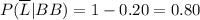
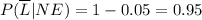
From the question, we know that

`\\ P(CN) = 0.30`

`\\ P(BB) = 0.10`

`\\ P(NE) = 0.60`

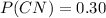
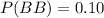
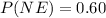
The probability of not being late is

`\\ P(\overline{L}) = P(\overline{L}|CN)*P(CN) + P(\overline{L}|BB)*P(BB) + P(\overline{L}|NE)*P(NE)`

`\\ P(\overline{L}) = 0.50*0.30 + 0.80*0.10 + 0.95*0.60`

`\\ P(\overline{L}) = 0.80`

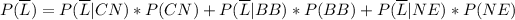
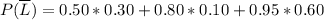
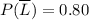
We are asked for

`\\ P(CN|\overline{L}) = \frac{P(CN \cap \overline{L})}{P(\overline{L})}`.

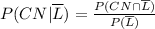But, like in the previous question

`\\ P(CN \cap \overline{L}) = P(\overline{L} \cap CN) = P(\overline{L}|CN)*P(CN) = 0.50*0.30`

Then

`\\ P(CN|\overline{L}) = (0.50*0.30)/(0.80)`

`\\ P(CN|\overline{L}) = (0.15)/(0.80)`

`\\ P(CN|\overline{L}) = 0.1875`

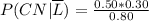
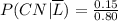
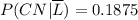
Then, the probability that Brian took a Commuter North bus (given that he was not late) is
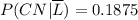`\\ P(CN|\overline{L}) = 0.1875`.

Answer 2

a) P(C/L) = 0.6668

b) P(C/L') = 0.1875

Explanation:

Let's call C the event that Brian takes Commuter North, B the event that Brian takes Bursley Baits, N the event that Brian takes Northwood Express, L the event that Brian is late and L' the event that Brian is not late.

First, there is equal probability of taking any given bus so, P(C)=P(B)=P(N)=1/3

Now, the probability P(C/L') that Brian took a Commuter North bus given that he is late is calculated as:

P(C/L) = P(C∩L)/P(L)

Where P(L) = P(C∩L) + P(B∩L) + P(N∩L)

Then, the probability P(C∩L) that Brian takes a Commuter North bus and it is late is calculated as:

P(C∩L)= (1/3)*(0.5) = 0.1667

Because, there is a probability of 1/3 to takes Commuter North Bus and if Brian takes Commuter North there is a 0.5 chance to be late.

At the same way, we get:

P(B∩L) = (1/3)(0.2) = 0.0667

P(N∩L) = (1/3)(0.05) = 0.0167

So, P(L) and P(C/L) are equal to:

P(L) = 0.1667 + 0.0667 + 0.0167 = 0.25

P(C/L) = 0.1667/0.25 = 0.6668

For part b, the probabilities of C, B and N changes and are equal to:

P(C) = 0.3

P(B) = 0.1

P(N) = 0.6

Then, the probability P(C/L') that he took a Commuter North bus given that Brian was not late to class is calculated as:

P(C/L') = P(C∩L')/P(L')

Where P(L') = P(C∩L') + P(B∩L') + P(N∩L')

So, P(C∩L'), P(B∩L') and P(N∩L') are equal to:

P(C∩L') = 0.3*(0.5) = 0.15

P(B∩L') = 0.1*(0.8) = 0.08

P(N∩L') = 0.6*(0.95) = 0.57

It means that P(L') and P(C/L') are equal to:

P(L') = 0.15 + 0.08 + 0.57 = 0.8

P(C/L') = 0.15/0.8 = 0.1875