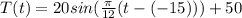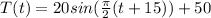Answer:
The model of the F-sharp note is
The model of the temperature is
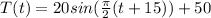
Explanation:
From the question we are told that
The frequency is
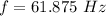
The Amplitude is A = 1
The phase shift is
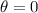
The angular velocity of a wave can be given as
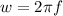
Substituting values
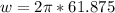
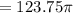
Now the sine function model of this note is given as
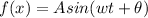
Substituting values
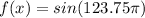
The minimum temperature is
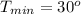
The maximum temperature is
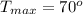
The average temperature is
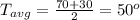
The Amplitude is

The period = 24 This because the function is modeled in such a way that 24 hour is time to complete a full cycle
The General sin equation is mathematically given as
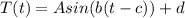
Where A is the Amplitude = 20
b is the angular speed
c is the phase shift
d is the vertical transition
And T(t) is the temperature after time t
And the period is evaluates as
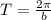 since
since
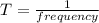
This implies that
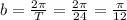
Since average is at 50 then it means that the wave graph has been shifted by 50 unites
d = 50
Now from our question
t = 3 hours when T(t) = 30
This means that
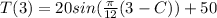
=>
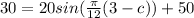
=>
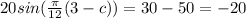
=>

Since
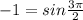 we have
we have
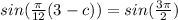
=>
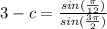
=>
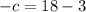
=>
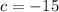
Therefore the sinusoidal model of the temperature is