Answer:
Explanation:
If I'm understanding this correctly, your problem is as follows:
The area of a circle is given by the formula
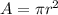
The area of the circle is changing at a rate of
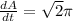 . Find the rate of change of the radius,
. Find the rate of change of the radius,
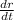 , when r = 8.
, when r = 8.
Assuming that is what you are asking, we will begin by finding the derivative of the area of a circle using implicit differentiation.

Filling in what we have:
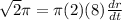 which simplifies a bit to
which simplifies a bit to
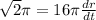
Divide both sides by 16π to get:

The π's cancel leaving the rate of change of the radius as
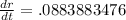 inches per second
inches per second