Question

Suppose that f(x)=e^{-x} for 0 < x. Determine the cumulative distribution function. Find the value of the cumulative distribution function at x=2.17. Round answer to 3 decimal places.

Answer 1

0.885822383089

Explanation:

Since it is focused on f(x), we would use the formula: 1-e^-(landa)(x). Landa is the one that looks like an arm with two legs. Here, landa=1, and x=2.7 so the formula would be 1-e^-2.17.

Answer 2

The correct answer is 0.886.

Explanation:

An exponential function with parameter K is given by

g (x) = K ×
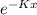`e^(-Kx)` for x > 0.

If we put the value of K = 1, we get the given function f (x) =
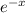`e^(-x)` for x > 0.

Now the cumulative distribution of an exponential function g is given by integrating the function g with respect to x.

G (x; K) = 1 -
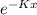`e^(-Kx)` for x > 0.

The cumulative distribution function of f is given by

F (x; K) = 1 -
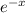`e^(-x)` for x > 0.

The value of cumulative function at x = 2.17 is given by 0.886.