Answer:
The electrical power is 96.5 W/m^2
Step-by-step explanation:
The energy balance is:
Ein-Eout=0

if:
Gsky=oTsky^4
Eb=oTs^4
qc=h(Ts-Tα)
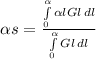
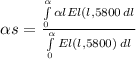
if Gl≈El(l,5800)
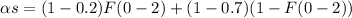
lt= 2*5800=11600 um-K, at this value, F=0.941
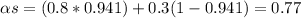
The hemispherical emissivity is equal to:

lt=2*333=666 K, at this value, F=0
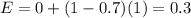
The hemispherical absorptivity is equal to:
