Question

Nike claims that the number of miles a jogger can get a on a pair of Nike’s running shoes is higher than 1000. Moreover, Nike also claims that their shoes outperform Adidas shoes by more than 15 miles. We have samples of 150 joggers using Nike shoes and 170 using Adidas shoes. The sample average of miles they got are 1015 for Nike and 995 for Adidas. The sample standard deviations are 100 for Nike and 50 for Adidas.

a.) At a 5% level of significance, is there statistical evidence showing that Nike shoes get more than 1000 miles?

b.) Obtain the p-value for the previous test. What does it mean?

c.) At a 5% level of significance, is there statistical evidence showing that Nike shoes outperform Adidas shoes?

d.) Obtain the p-value for the previous test. Interpret.

Answer 1

a) There is statistical evidence showing that Nike shoues get more than 1000 miles.

b) The p-value of t=1.84 and df=149 is P=0.034.

It represents the probability of getting this sample results if the population parameters are the ones from the null hypothesis.

In this case, the low p-value shows is rare to get a sample of n=150 and mean 1015 miles, if the population mean is 1000. This is evidence that the null hypothesis is not true.

c) There is no enough evidence to claim that Nike shoes outperform Adidas shoes by 15 miles.

d) The p-value for t=0.55 and 318 df is P=0.29.

This shows that there is a probability of P=0.29 of getting samples that show this difference if the statement of the null hypothesis is true.

Explanation:

a) We have to perform a hypothesis test with the following hypothesis:

`H_0: \mu\leq 1000\\\\H_a: \mu>1000`

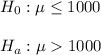
The level of significance is 0.05.

The sample mean is 1015 and the sample standard deviation is 100.

The degrees of freedom are df = 150-1 = 149.

The t-statistic is:

`t=(M-\mu)/(s/√(n))=(1015-1000)/(100/√(150)) =(15)/(8.165) =1.84`

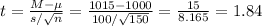
The critical value for t is t=1.66. As the t-statistic is bigger than the critical t, it falls in the rejection region. The null hypothesis is rejected.

There is statistical evidence showing that Nike shoues get more than 1000 miles.

b) The p-value of t=1.84 and df=149 is P=0.034.

It represents the probability of getting this sample results if the population parameters are the ones from the null hypothesis.

In this case, the low p-value shows is rare to get a sample of n=150 and mean 1015 miles, if the population mean is 1000. This is evidence that the null hypothesis is not true.

c) In this case, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2\leq 15\\\\H_a: \mu_1-\mu_2>15`

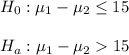
The significance level is 0.05.

The difference between sample means is:

`M_d=1015-995=20`

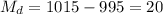
The standard deviation of the difference is:

`\sigma=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}= \sqrt{(100^2)/(150)+(50^2)/(170)}= √(66.67+14.70)=9`

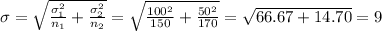
The degrees of freedom are:

`df=n_1+n_2-2=150+170-2=318`

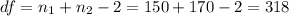
The critical value is t=1.65

The t-statistic is:

`t=(M_d-(\mu_1-\mu_2))/(\sigma) =(20-15)/(9)= (5)/(9)= 0.55`

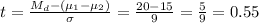
The value ot the t-statistic is lower than the critical value, so it lies within the acceptance region.

There is no enough evidence to claim that Nike shoes outperform Adidas shoes by 15 miles.

d) The p-value for t=0.55 and 318 df is P=0.29.

This shows that there is a probability of P=0.29 of getting samples that show this difference if the statement of the null hypothesis is true.