Answer:
129 km/hr
Step-by-step explanation:
Distance of Car A North of the Intersection, y=0.3km
Distance of Car B West of the Intersection, x=0.4 km
The distance z, between A and B is determined by the Pythagoras theorem
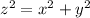

Taking derivative of
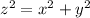
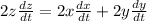
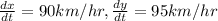

The distance z, between the cars is changing at a rate of 129 km/hr.