Question

Scores on the Wechsler intelligence quotient (IQ) test for adults have a normal probability distribution with a mean score of 100 and a standard deviation of 15 points. The US military has minimum enlistment standards at about an IQ score of 85. Based on IQ scores only, what is the probability that a randomly selected adult does not meet US military enlistment standards

Answer 1

Probability = 0.1587

Explanation:

The provided information is:

Let X be the scores of the IQ test for adults that is normally distributed with mean
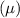`(\mu)` = 100 and standard deviation
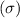`(\sigma)` = 15.

Also, US military has minimum IQ score of 85.

Thus, the probability that randomly selected adult does not meet US military enlistment standards is:
`P(X<85)`

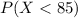
The probability can also be written as:

`P(X < x) =P(Z<(x-\mu)/(\sigma))`

Thus,

`P(X<85)=P(Z<(85-100)/(15))\\\\=P(Z<-1)`

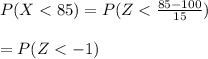
Using the Normal probability table probability of Z = -1 is 0.1587

Thus, the required probability is 0.1587